microstructpy.geometry.Ellipse¶
- class microstructpy.geometry.Ellipse(**kwargs)[source]¶
Bases:
objectA 2-D ellipse geometry.
This class contains a 2-D ellipse. It is defined by a center point, axes and an orientation.
Without any parameters, the ellipse defaults to a unit circle.
- Parameters
a (float) – (optional) Semi-major axis of ellipse. Defaults to 1.
b (float) – (optional) Semi-minor axis of ellipse. Defaults to 1.
center (list) – (optional) The ellipse center. Defaults to (0, 0).
axes (list) – (optional) A 2-element list of semi-axes, equivalent to
[a, b]. Defaults to [1, 1].size (float) – (optional) The diameter of a circle with equivalent area. Defaults to 1.
aspect_ratio (float) – (optional) The ratio of x-axis to y-axis length. Defaults to 1.
angle (float) – (optional) The counterclockwise rotation angle, in degrees, measured from the +x axis.
angle_deg (float) – (optional) The rotation angle, in degrees.
angle_rad (float) – (optional) The rotation angle, in radians.
matrix (numpy.ndarray) – (optional) The 2x2 rotation matrix.
orientation (numpy.ndarray) – (optional) Alias for
matrix.
- approximate(x1=None)[source]¶
Approximate ellipse with a set of circles.
This function converts an ellipse into a set of circles. It implements a published algorithm by Ilin and Bernacki. 1
Example
>>> import matplotlib.pyplot as plt >>> import microstructpy as msp >>> import numpy as np >>> ellipse = msp.geometry.Ellipse(a=3, b=1) >>> approx = ellipse.approximate(0.7) >>> approx array([[ 0. , 0. , 1. ], [ 0.7 , 0. , 0.96889112], [ 1.38067777, 0. , 0.87276349], [ 2.00213905, 0. , 0.7063497 ], [ 2.5234414 , 0. , 0.45169729], [ 2.66666667, 0. , 0.33333333], [-0.7 , 0. , 0.96889112], [-1.38067777, 0. , 0.87276349], [-2.00213905, 0. , 0.7063497 ], [-2.5234414 , 0. , 0.45169729], [-2.66666667, 0. , 0.33333333]]) >>> ellipse.plot(edgecolor='k', facecolor='none', lw=3) >>> t = np.linspace(0, 2 * np.pi) >>> for x, y, r in approx: ... plt.plot(x + r * np.cos(t), y + r * np.sin(t), 'b') >>> plt.xticks(np.unique(np.concatenate((approx[:, 0], (-3, 3))))) >>> plt.yticks(np.unique(np.concatenate((approx[:, 1], (-1, 1))))) >>> plt.axis('scaled') >>> plt.grid(True, linestyle=':') >>> plt.show()
Executing the code above produces Fig. 28.
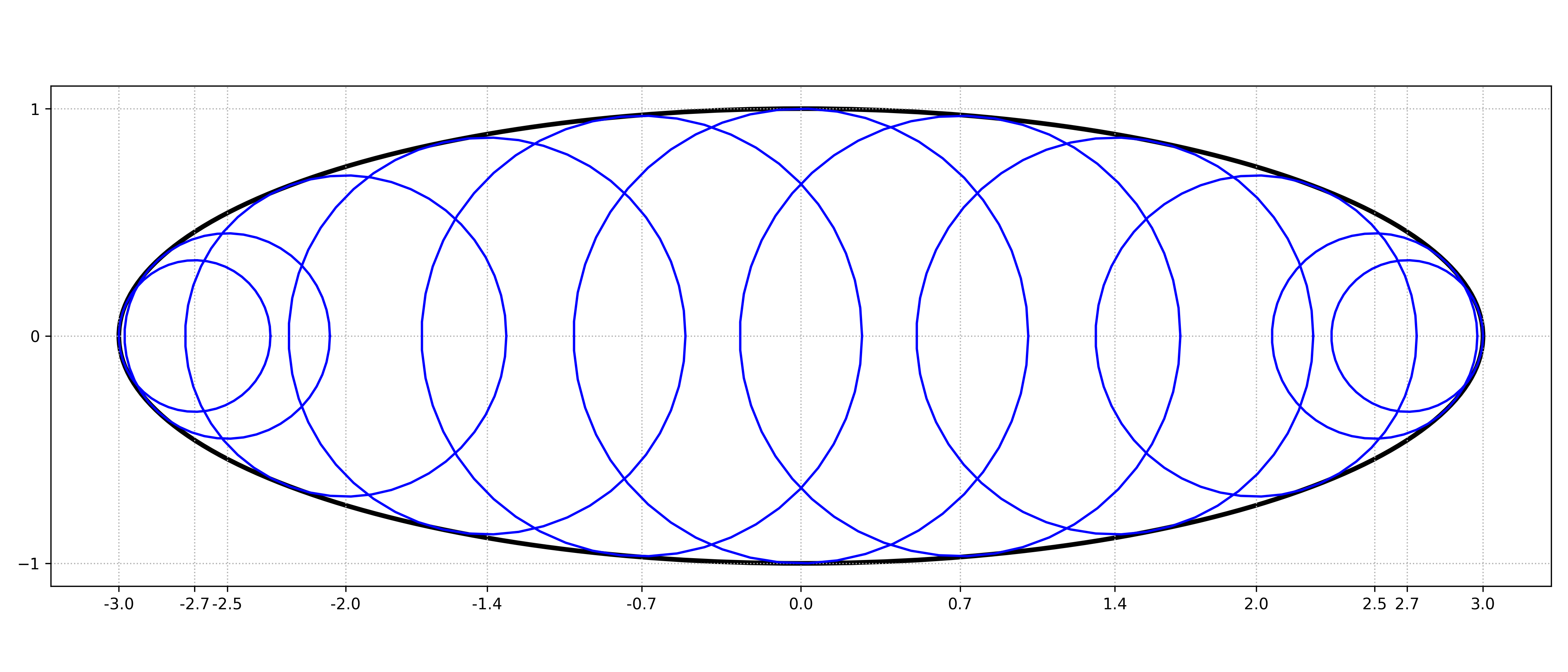
Fig. 28 Circular approximation of ellipse, after Ilin and Bernacki.¶
- Parameters
x1 (float or None) – (optional) Position of the first circle along the +x axis. Defaults to 0.5x the shortest semi-axis.
- Returns
An Nx3 list of the (x, y, r) data of each circle approximating the ellipse.
- Return type
- Raises
AssertionError – Thrown if max(a, b) < x1.
- 1
Ilin, D.N., and Bernacki, M., “Advancing Layer Algorithm of Dense Ellipse Packing for Generating Statistically Equivalent Polygonal Structures,” Granular Matter, vol. 18(3), pp. 43, 2016.
- classmethod area_expectation(**kwargs)[source]¶
Expected value of area.
This function computes the expected value for the area of an ellipse. The keyword arguments are the same as the input parameters of the class. The keyword values can be either constants (ints or floats) or distributions from the SciPy
scipy.statsmodule.If an ellipse is specified by size, the expected value is computed as follows.
\[\begin{split}\mathbb{E}[A] &= \frac{\pi}{4} \mathbb[S^2] \\ &= \frac{\pi}{4} (\mu_S^2 + \sigma_S^2)\end{split}\]If the ellipse is specified by independent distributions for each semi-axis, the expected value is computed by:
\[\mathbb{E}[A] = \pi\, \mathbb{E}[A B] = \pi \mu_A \mu_B\]If the ellipse is specified by the second semi-axis and the aspect ratio, the expected value is computed by:
\[\begin{split}\mathbb{E}[A] &= \pi\, \mathbb{E}[K B^2] \\ &= \pi \mu_K (\mu_B^2 + \sigma_B^2)\end{split}\]Finally, if the ellipse is specified by the first semi-axis and the aspect ratio, the expected value is computed by Monte Carlo:
\[\begin{split}\mathbb{E}[A] &= \pi\, \mathbb{E}\left[\frac{A^2}{K}\right] \\ &\approx \frac{\pi}{n} \sum_{i=1}^n \frac{A_i}{K_i}\end{split}\]where \(n=1000\).
- Parameters
**kwargs – Keyword arguments, see
microstructpy.geometry.Ellipse.- Returns
Expected value of the area of the ellipse.
- Return type
- best_fit(points)[source]¶
Find ellipse of best fit for points
This function computes the ellipse of best fit for a set of points. It calls the least-squares-ellipse-fitting package, which implements a published fitting algorithm in Python. 2
The current instance of the class is used as an initial guess for the ellipse of best fit. Since an ellipse can be expressed multiple ways (e.g. rotate 90 degrees and flip the axes), this initial guess is used to choose from the multiple parameter sets.
- Parameters
points (list or numpy.ndarray) – An Nx2 list of points to fit.
- Returns
An instance of the class that best fits the points.
- Return type
- 2
Halir, R., Flusser, J., “Numerically Stable Direct Least Squares Fitting of Ellipses,” 6th International Conference in Central Europe on Computer Graphics and Visualization, Vol. 98, 1998. (http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1.7559&rep=rep1&type=pdf)
- plot(**kwargs)[source]¶
Plot the ellipse.
This function adds a
matplotlib.patches.Ellipsepatch to the current axes using matplotlib. The keyword arguments are passed to the patch.- Parameters
**kwargs (dict) – Keyword arguments for matplotlib.
- reflect(points)[source]¶
Reflect points across surface.
This function reflects a point or set of points across the surface of the ellipse. Points at the center of the ellipse are not reflected.
- Parameters
points (list or numpy.ndarray) – Nx2 list of points to reflect.
- Returns
Reflected points.
- Return type
- within(points)[source]¶
Test if points are within ellipse.
This function tests whether a point or set of points are within the ellipse. For the set of points, a list of booleans is returned to indicate which points are within the ellipse.
- Parameters
points (list or numpy.ndarray) – Point or list of points.
- Returns
Set to True for points in ellipse.
- Return type
- property matrix¶
Rotation matrix
- Type
- property orientation¶
Rotation matrix
- Type
- property volume¶
Same as
microstructpy.geometry.Ellipse.area- Type