microstructpy.geometry.Rectangle¶
- class microstructpy.geometry.Rectangle(**kwargs)[source]¶
Bases:
microstructpy.geometry.n_box.NBoxThis class contains a generic, 2D rectangle. The position and dimensions of the box can be specified using any of the parameters below.
Without parameters, this returns a unit square centered on the origin.
- Parameters
length (float) – (optional) Length of the rectangle.
width (float) – (optional) Width of the rectangle. (optional)
side_lengths (list) – (optional) Side lengths. Defaults to (1, 1).
center (list) – (optional) Center of rectangle. Defaults to (0, 0).
corner (list) – (optional) Bottom-left corner.
bounds (list) – (optional) Bounds of rectangle. Expected to be in the format [(xmin, xmax), (ymin, ymax)].
limits – Alias for bounds.
angle (float) – (optional) The rotation angle, in degrees.
angle_deg (float) – (optional) The rotation angle, in degrees.
angle_rad (float) – (optional) The rotation angle, in radians.
matrix (numpy.ndarray) – (optional) The 2x2 rotation matrix.
- approximate(x1=None)[source]¶
Approximate rectangle with a set of circles.
This method approximates a rectangle with a set of circles. These circles are spaced uniformly along the long axis of the rectangle with distance
x1between them.Example
For a rectangle with length=2.5, width=1, and x1=0.3, the approximation would look like Fig. 29.
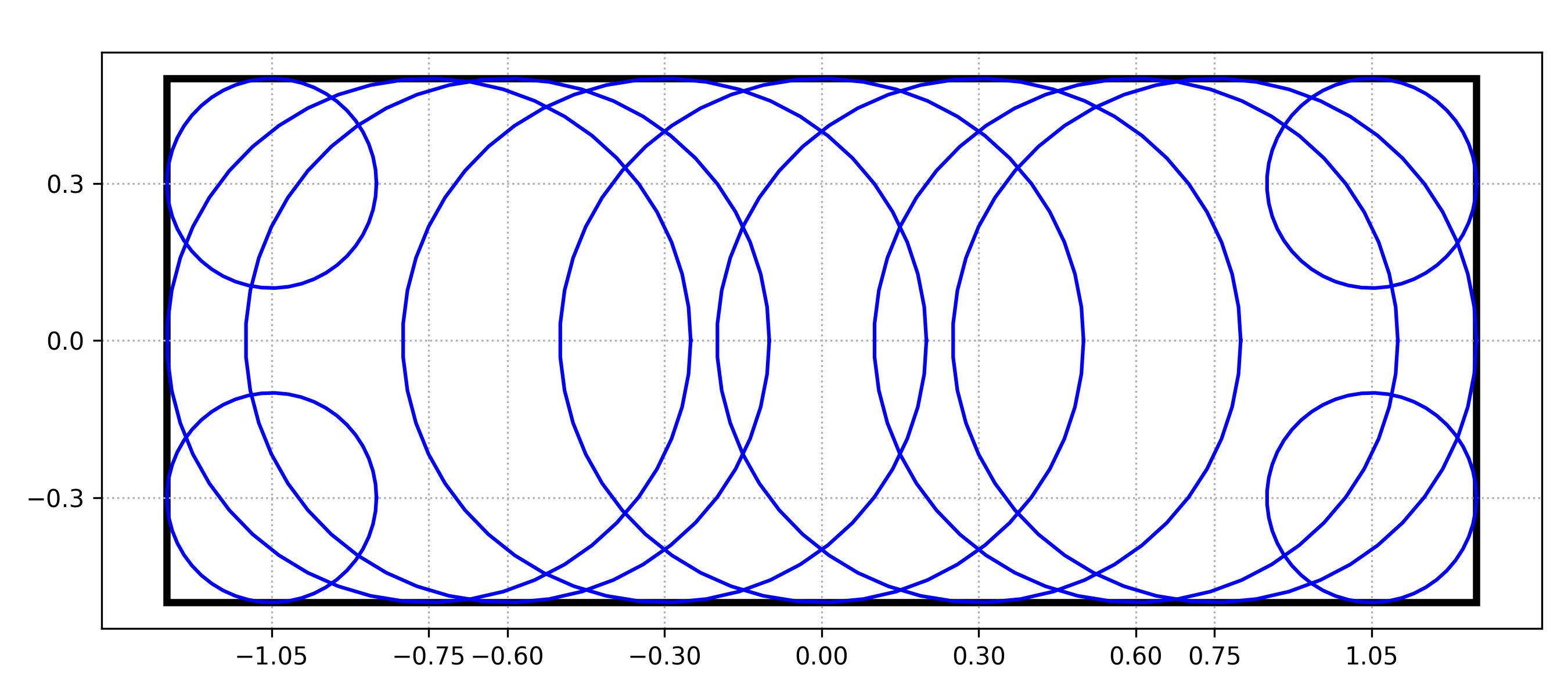
Fig. 29 Circular approximation of rectangle.¶
- classmethod area_expectation(**kwargs)[source]¶
Expected area of rectangle
This method computes the expected area of a rectangle. There are two main ways to define the size of a rectangle: by the length and width and by the bounds. If the input rectangle is defined by length and width, the expected area is:
\[\mathbb{E}[A] = \mathbb{E}[L W] = \mu_L \mu_W\]For the case where it is defined by upper and lower bounds:
\[\mathbb{E}[A] = \mathbb{E}[(X_U - X_L) (Y_U - Y_L)]\]\[\mathbb{E}[A] = \mu_{X_U}\mu_{Y_U} - \mu_{X_U} \mu_{Y_L} - \mu_{X_L}\mu_{Y_U} + \mu_{X_L}\mu_{Y_L}\]Example
>>> import scipy.stats >>> import microstructpy as msp >>> L = scipy.stats.uniform(loc=1, scale=2) >>> W = scipy.stats.norm(loc=3.2, scale=5.1) >>> L.mean() * W.mean() 6.4 >>> msp.geometry.Rectangle.area_expectation(length=L, width=W) 6.4
- Parameters
**kwargs – Keyword arguments, same as
Rectanglebut the inputs can be from thescipy.statsmodule.- Returns
Expected/average area of rectangle.
- Return type
- plot(**kwargs)[source]¶
Plot the rectangle.
This function adds a
matplotlib.patches.Rectanglepatch to the current axes. The keyword arguments are passed through to the patch.- Parameters
**kwargs (dict) – Keyword arguments for the patch.
- within(points)¶
Test if points are within n-box.
This function tests whether a point or set of points are within the n-box. For the set of points, a list of booleans is returned to indicate which points are within the n-box.
- Parameters
points (list or numpy.ndarray) – Point or list of points.
- Returns
Flags set to True for points in geometry.
- Return type