Uniform Seeding Voronoi Diagram¶
Python Script¶
The basename for this file is uniform_seeding.py.
The file can be run using this command:
microstructpy --demo=uniform_seeding.py
The full text of the script is:
from __future__ import division
import os
import matplotlib as mpl
import numpy as np
from matplotlib import pyplot as plt
from scipy.spatial import distance
import microstructpy as msp
# Create domain
domain = msp.geometry.Square(corner=(0, 0))
# Create list of seed points
factory = msp.seeding.Seed.factory
n = 200
seeds = msp.seeding.SeedList([factory('circle', r=0.007) for i in range(n)])
# Position seeds according to Mitchell's Best Candidate Algorithm
np.random.seed(0)
lims = np.array(domain.limits) * (1 - 1e-5)
centers = np.zeros((n, 2))
for i in range(n):
f = np.random.rand(i + 1, 2)
pts = f * lims[:, 0] + (1 - f) * lims[:, 1]
try:
min_dists = distance.cdist(pts, centers[:i]).min(axis=1)
i_max = np.argmax(min_dists)
except ValueError: # this is the case when i=0
i_max = 0
centers[i] = pts[i_max]
seeds[i].position = centers[i]
# Create Voronoi diagram
pmesh = msp.meshing.PolyMesh.from_seeds(seeds, domain)
# Set colors based on area
areas = pmesh.volumes
std_area = domain.area / n
min_area = min(areas)
max_area = max(areas)
cell_colors = np.zeros((n, 3))
for i in range(n):
if areas[i] < std_area:
f_red = (areas[i] - min_area) / (std_area - min_area)
f_green = (areas[i] - min_area) / (std_area - min_area)
f_blue = 1
else:
f_red = 1
f_green = (max_area - areas[i]) / (max_area - std_area)
f_blue = (max_area - areas[i]) / (max_area - std_area)
cell_colors[i] = (f_red, f_green, f_blue)
# Create colorbar
vs = (std_area - min_area) / (max_area - min_area)
colors = [(0, (0, 0, 1)), (vs, (1, 1, 1)), (1, (1, 0, 0))]
cmap = mpl.colors.LinearSegmentedColormap.from_list('area_cmap', colors)
norm = mpl.colors.Normalize(vmin=min_area, vmax=max_area)
sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
cb = plt.colorbar(sm, ticks=[min_area, std_area, max_area], ax=plt.gca(),
orientation='horizontal', fraction=0.046, pad=0.08)
cb.set_label('Cell Area')
# Plot Voronoi diagram and seed points
pmesh.plot(edgecolors='k', facecolors=cell_colors)
seeds.plot(edgecolors='k', facecolors='none')
plt.axis('square')
plt.xlim(domain.limits[0])
plt.ylim(domain.limits[1])
# Save diagram
file_dir = os.path.dirname(os.path.realpath(__file__))
filename = os.path.join(file_dir, 'uniform_seeding/voronoi_diagram.png')
dirs = os.path.dirname(filename)
if not os.path.exists(dirs):
os.makedirs(dirs)
plt.savefig(filename, bbox_inches='tight', pad_inches=0)
Domain¶
The domain of the microstructure is a Square.
Without arguments, the square’s center is (0, 0) and side length is 1.
Seeds¶
A set of 200 seed circles with small radius is initially created. The positions of the seeds are set with Mitchell’s Best Candidate Algorithm 1. This algorithm positions seed i by sampling i + 1 random points and picking the one that is furthest from its nearest neighbor.
Polygon Mesh¶
A polygon mesh is created from the list of seed points using the
from_seeds() class method.
Plotting¶
The facecolor of each polygon is determined by its area. If it is below the standard area (domain area / number of cells), then it is shaded blue. If it is above the standard area, it is shaded red. A custom colorbar is added to the figure and it is saved as a PNG, shown in Fig. 21.
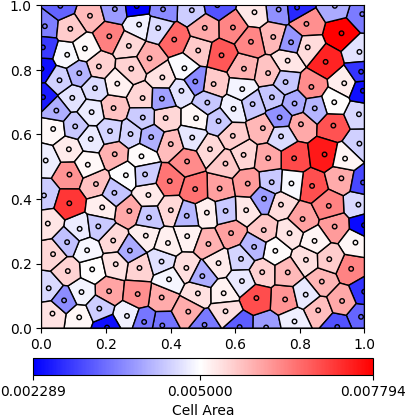
Fig. 21 Uniformly seeded Voronoi diagram with cells colored by area.¶
- 1
Mitchell, T.J., “An Algorithm for the Construction of “D-Optimal” Experimental Designs,” Technometrics, Vol. 16, No. 2, May 1974, pp. 203-210. (https://www.jstor.org/stable/1267940)